Sito di CalcS

Abbiamo già visto come il metodo dei giunti reali posizionati sia una strategia per convertire un modello FEM unifilare in un progetto esecutivo e rigoroso.

In questa pagina entriamo nel dettaglio di un concetto (quello di connettività) che è importante per CalcS. In particolare è importante distinguere tra:

• connettività esplicita (o naturale) e,
• connettività implicita (o inferita).

Consideriamo il semplice modello ad elementi finiti in figura seguente, ed analizziamo per esempio il beam 711. Il beam 711 (verde) ha il nodo iniziale in comune con gli elementi 525 e 526.

Diremo allora che c'è connettività esplicita o connettività naturale:

La connettività naturale è la condivisione tra due o più elementi finiti di un nodo del modello strutturale. Tale condivisione implica che uno o più gradi di libertà siano in comune tra gli elementi connessi.

la connettività naturale si dice anche "esplicita" perchè è scritta in maniera chiaramente leggibile nella matrice di connettività degli elementi finiti.

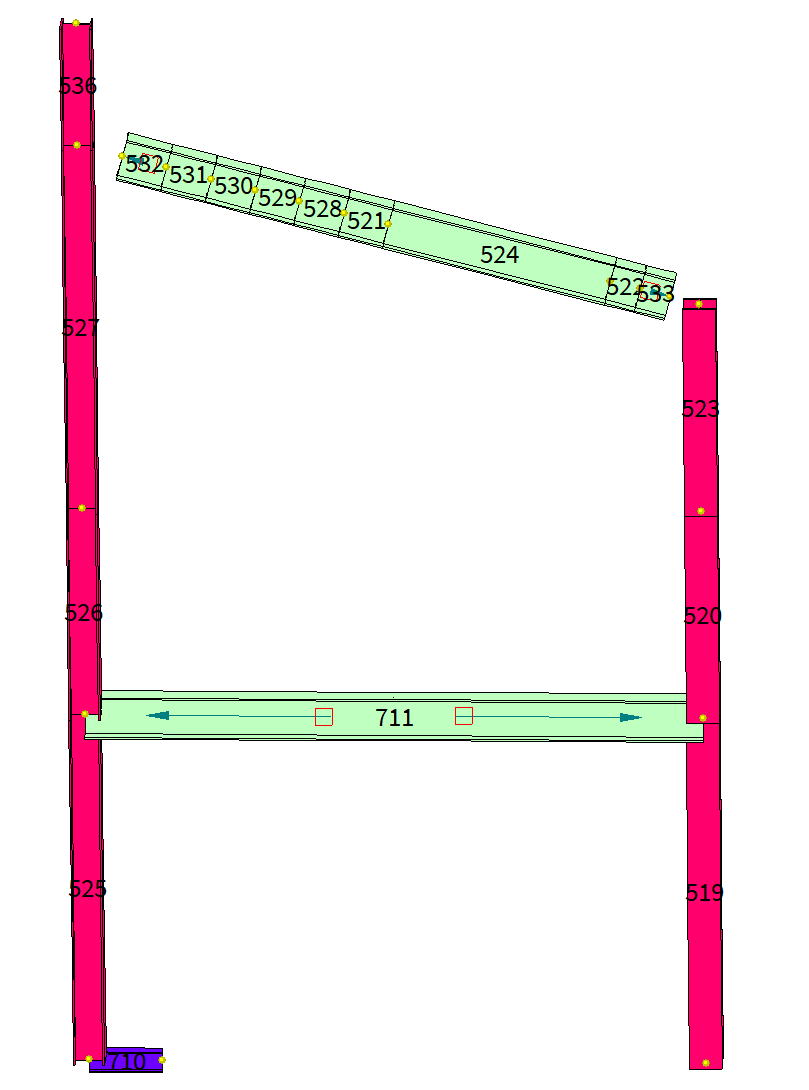
Consideriamo invece l'elemento 532: esso non ha alcun nodo in comune con la colonna formata da 536 e 527. In generale diremmo che non vi è condivisione di gradi di libertà tra questi elementi. Tuttavia i moderni software ad elementi finiti commerciali

hanno "sofisticati modi alternativi alla connettività naturale" per collegare diverse parti di struttura, ad esempio:

• link rigidi (elementi definiti per via cinematica che collegano due nodi del modello),
• definizioni dirette di legame tra gradi di libertà nel sistema di equazioni collegato al modello strutturale,
• relazioni di contatto lineare o non lineare (che servono ad esempio per simulare l'urto di una struttura contro l'altra e che si attivano sotto determinate condizioni scelte dall'utente).

Non è lo scopo di CalcS discutere queste modalità sofisticate di connettere gli elementi senza la condivisione di un nodo tra di loro, ciascun software FEM ha le sue definizioni, i suoi scopi ed i suoi algoritmi. Inoltre CalcS importa gli elementi finiti, che sono concetti trasversali ai diversi software, e non i "sofisticati modi alternativi alla connettività naturale" propri di ciascuna implementazione.

Rimane tuttavia il fatto che a CalcS potrebbe essere richiesto di posizionare nella prima estremità dell'elemento 532 un nodo di tipo RJ_2(ad esempio).

Rappresentiamo questo concetto nella seguente immagine:

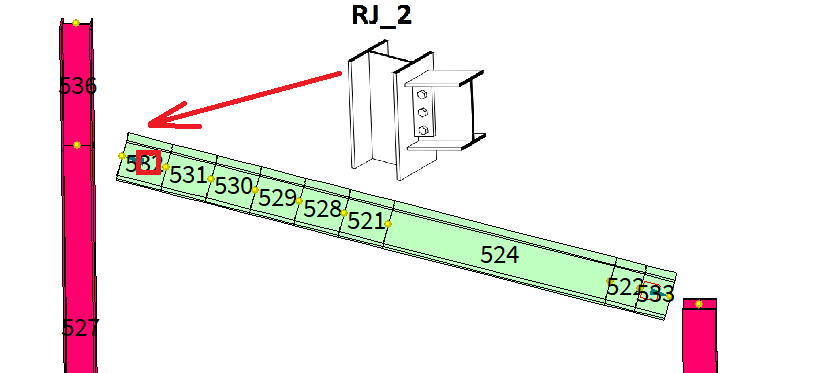
CalcS allora avrà ricevuto una istruzione molto esplicita: la trave verde deve connettersi a qualcosa per poter esprimere la connessione richiesta, per richiesta del progettista.

E' per questo che CalcS scansionerà l'intorno della trave verde 532 per cercare una colonna coerente con il nodo che è stato richiesto. Se la colonna non viene trovata, il nodo sarà incalcolabile. Se la colonna dovesse essere trovata CalcS prolungherà la trave fino ad incontrare l'asse della colonna, e tale prolungamento potrà incontrare la colonna sia in corrispondenza di un nodo FEM, sia relativamente lontano da un nodo FEM, come rappresentato in figura seguente. Sia la alternativa "A" (prolungamento che si incontra in un nodo FEM) sia le alternative "B" o "C" sono ammissibili per CalcS nel cercare di adempiere alla richiesta di calcolo di una connessione RJ_2 nell'intorno dell'elemento 532.

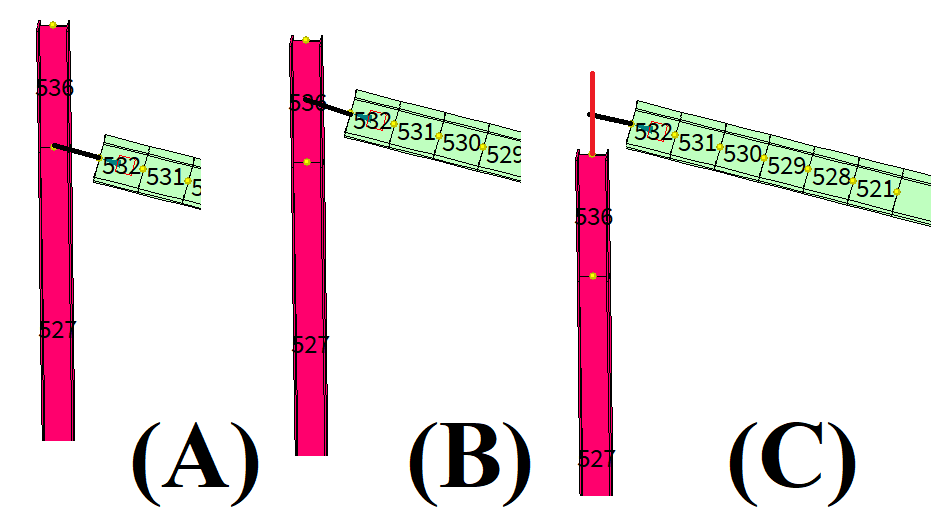
Diremo allora che c'è connettività implicita o connettività inferita:

La connettività implicita è la relazione tra due o più elementi finiti nell'intorno di una posizione del modello strutturale. Tale relazione implica che uno o più gradi di libertà siano in comune tra gli elementi connessi, mediante "operatori di connettività specifici al modello strutturale" ignoti a CalcS, ma che il progettista conferma di aver correttamente impiegato quando richiede nell'intorno di uno o più degli elementi da collegare la presenza di un giunto reale posizionato che implica la sussistenza di tale relazione.

La connettività implicità è tollerante in geometria: piccoli disassamenti o fuori piano vengono interpretati come ammissibili e non precludono il calcolo del nodo!

Se siete arrivati a leggere fin qui, sappiate che ci farebbe piacere un vostro feedback sulla nostra fagina facebook: https://www.facebook.com/CalcSsoftware  .

Se siete arrivati a leggere fin qui, vi consigliamo di proseguire leggendo ID di dettaglio in CalcS (il demone dei dettagli).